College Algebra Textbook, Test Bank

College Algebra TextBook by OpenStax plus MCQ, Essay Questions & Key Terms

College Algebra provides a comprehensive exploration of algebraic principles and meets scope and sequence requirements for a typical introductory algebra course. The modular approach and richness of content ensure that the book meets the needs of a variety of courses. College Algebra offers a wealth of examples with detailed, conceptual explanations, building a strong foundation in the material before asking students to apply what they’ve learned.

* Complete Textbook by OpenStax

* Multiple Choices Questions (MCQ)

* Essay Questions Flash Cards

* Key-Terms Flash Cards

Powered by QuizOver.com the leading online quiz creator

https://www.quizover.com

1. Prerequisites

Introduction to Prerequisites

1.1. Real Numbers: Algebra Essentials

1.2. Exponents and Scientific Notation

1.3. Radicals and Rational Exponents

1.4. Polynomials

1.5. Factoring Polynomials

1.6. Rational Expressions

2. Equations and Inequalities

Introduction to Equations and Inequalities

2.1. The Rectangular Coordinate Systems and Graphs

2.2. Linear Equations in One Variable

2.3. Models and Applications

2.4. Complex Numbers

2.5. Quadratic Equations

2.6. Other Types of Equations

2.7. Linear Inequalities and Absolute Value Inequalities

3. Functions

Introduction to Functions

3.1. Functions and Function Notation

3.2. Domain and Range

3.3. Rates of Change and Behavior of Graphs

3.4. Composition of Functions

3.5. Transformation of Functions

3.6. Absolute Value Functions

3.7. Inverse Functions

4. Linear Functions

Introduction to Linear Functions

4.1. Linear Functions

4.2. Modeling with Linear Functions

4.3. Fitting Linear Models to Data

5. Polynomial and Rational Functions

Introduction to Polynomial and Rational Functions

5.1. Quadratic Functions

5.2. Power Functions and Polynomial Functions

5.3. Graphs of Polynomial Functions

5.4. Dividing Polynomials

5.5. Zeros of Polynomial Functions

5.6. Rational Functions

5.7. Inverses and Radical Functions

5.8. Modeling Using Variation

6. Exponential and Logarithmic Functions

Introduction to Exponential and Logarithmic Functions

6.1. Exponential Functions

6.2. Graphs of Exponential Functions

6.3. Logarithmic Functions

6.4. Graphs of Logarithmic Functions

6.5. Logarithmic Properties

6.6. Exponential and Logarithmic Equations

6.7. Exponential and Logarithmic Models

6.8. Fitting Exponential Models to Data

7. Systems of Equations and Inequalities

Introduction to Systems of Equations and Inequalities

7.1. Systems of Linear Equations: Two Variables

7.2. Systems of Linear Equations: Three Variables

7.3. Systems of Nonlinear Equations and Inequalities: Two Variables

7.4. Partial Fractions

7.5. Matrices and Matrix Operations

7.6. Solving Systems with Gaussian Elimination

7.7. Solving Systems with Inverses

7.8. Solving Systems with Cramer's Rule

8. Analytic Geometry

Introduction to Analytic Geometry

8.1. The Ellipse

8.2. The Hyperbola

8.3. The Parabola

8.4. Rotation of Axes

8.5. Conic Sections in Polar Coordinates

9. Sequences, Probability, and Counting Theory

Introduction to Sequences, Probability and Counting Theory

9.1. Sequences and Their Notations

9.2. Arithmetic Sequences

9.3. Geometric Sequences

9.4. Series and Their Notations

9.5. Counting Principles

9.6. Binomial Theorem

9.7. Probability

OpenStax artı MCQ, Kompozisyon Sorular ve Temel Terimler tarafından Koleji Cebir Ders Kitabı

Kolej Cebir cebirsel ilkelerin kapsamlı bir keşif sağlar ve tipik bir tanıtım cebir kursu için kapsam ve sıra gereksinimlerini karşılamaktadır. modüler yaklaşım ve içerik zenginliği kitap kurslarının çeşitli ihtiyaçlarını karşılayan emin olun. Kolej Cebir onlar öğrendiklerinizi uygulamak için öğrencilere istemeden önce malzemesinde sağlam bir temel inşa ayrıntılı kavramsal açıklamalar ile örnekler bir zenginlik sunuyor.

* OpenStax tarafından Komple Ders Kitabı

* Çoklu Seçimleri Sorular (MCQ)

* Deneme Soruları Flaş Kartları

* Anahtar Terimler Flaş Kartları

QuizOver.com önde gelen online bilgi yarışması yaratıcısı tarafından desteklenmektedir

https://www.quizover.com

1. Ön şartlar

Ön giriş

1.1. Gerçek Sayılar: Cebir Essentials

1.2. Üslü ve Bilimsel Gösterim

1.3. Radikaller ve Rasyonel Üslü

1.4. Polinomlar

1.5. faktoring Polinomlar

1.6. rasyonel İfadeler

2. Denklemler ve eşitsizlikler

Eşitlik ve Eşitsizlikler giriş

2.1. Dikdörtgen Sistemleri ve Grafikler Koordinat

2.2. Tek Değişkenli Doğrusal Denklemler

2.3. Modeller ve Uygulamaları

2.4. Karışık sayılar

2.5. İkinci dereceden denklemler

2.6. Denklem Diğer Türleri

2.7. Doğrusal Eşitsizlikler ve Mutlak Değer Eşitsizlikler

3. Fonksiyonlar

Fonksiyonlar Giriş

3.1. İşlevleri ve Gösterimi

3.2. Alan ve Range

3.3. Değişim Oranları ve Grafikler Davranış

3.4. İşlevleri Bileşimi

3.5. Fonksiyonlar dönüşümü

3.6. Mutlak Değer İşlevleri

3.7. Ters Fonksiyonlar

4. Doğrusal Fonksiyonlar

Doğrusal Fonksiyonlar giriş

4.1. Doğrusal Fonksiyonlar

4.2. Doğrusal Fonksiyonlar ile modelleme

4.3. Verilere Montaj Doğrusal Modeller

5. Polinom ve Rasyonel Fonksiyonlar

Polinomu ve Rasyonel Fonksiyonlar giriş

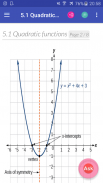
5.1. İkinci Dereceden Fonksiyonlar

5.2. Güç Fonksiyonlar ve Polinom Fonksiyonlar

5.3. Polinom Fonksiyonların Grafikleri

5.4. Çokterimliler bölündüğünde

5.5. Polinom Fonksiyonların sıfırları

5.6. rasyonel Fonksiyonlar

5.7. Tersi ve Radikal Fonksiyonlar

5.8. Varyasyon Kullanarak Modelleme

6. Üstel ve Logaritmik Fonksiyonlar

Üstel ve Logaritmik Fonksiyonlar giriş

6.1. Üstel Fonksiyonlar

6.2. Üstel Fonksiyonların Grafikleri

6.3. logaritmik Fonksiyonlar

6.4. Logaritmik Fonksiyonların Grafikleri

6.5. logaritmik Özellikleri

6.6. Üstel ve Logaritmik Denklemler

6.7. Üstel ve Logaritmik Modeller

6.8. Verilere Montaj Üstel Modeller

Eşitlik ve Eşitsizlikler 7. Sistemleri

Eşitlik ve Eşitsizlikler Sistemlerine Giriş

7.1. Lineer Denklem Sistemleri: İki Değişkenler

7.2. Lineer Denklem Sistemleri: Üç Değişkenler

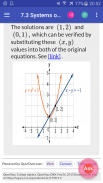
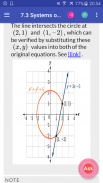
7.3. Doğrusal Olmayan Eşitlik ve Eşitsizlikler Sistemleri: İki Değişkenler

7.4. Kısmi kesirler

7.5. Matrisler ve Matris İşlemleri

7.6. Gauss Önlenmesi ile Sistemlerinin Çözümü

7.7. Tersler ile Çözme Sistemleri

7.8. Cramer Kuralı ile Sistemlerinin Çözümü

8. Analitik Geometri

Analitik Geometriye Giriş

8.1. Elips

8.2. Hiperbol

8.3. Parabol

8.4. Eksen Dönmesi

8.5. Polar koordinatlarda Konik Bölümler

9. Diziler, Olasılık ve Sayım Teori

Dizilerin giriş, Olasılık ve Sayma Teorisi

9.1. Diziler ve Onların Gösterimler

9.2. aritmetik Diziler

9.3. Geometrik Diziler

9.4. Seri ve Onların Gösterimler

9.5. İlkeleri Sayma

9.6. binom Teoremi

9.7. olasılık